HEXAEDRO APOYADO SOBRE UNA CARA EN EL PLANO HORIZONTAL:

DEFINICIÓN:

Se denomina poliedros a los cuerpos cuyas caras son polígonos regulares.  Estos son cinco, pero nosotros nos vamos a centrar en uno en particular, el hexaedro.

El hexaedro o cubo es un poliedro formado por seis caras que son cuadrados. Tiene doce aristas y ocho vértices. Además sus ángulos son rectos formando un triedro trirrectángulo.

REPRESENTACIÓN:

Si situamos una de las caras del hexaedro contenida en el plano horizontal, la cara opuesta se proyecta coincidente con ella y las cuatro restantes son proyectantes respecto al plano horizontal.

La proyección horizontal es un cuadrado de lado igual a la arista del cubo. Las caras horizontales se proyectan sobre el plano vertical en dos segmentos paralelos a la L.T. a una distancia igual a la arista. 

Lo vemos en la siguiente imagen donde se representa el hexaedro apoyado:

El Tetraedro se puede considerar como una pirámide recta y regular, de cuatro caras idénticas y cuya base, y por tanto sus caras laterales son triángulos equiláteros. Los lados de estos triángulos son las aristas de la superficie.

Dibujamos una de estas caras sobre el plano horizontal de proyección para una magnitud arbitraria de la arista y completamos esta vista dibujando la proyección del vértice superior V que coincide con el centro del triángulo.

Para dibujar la proyección vertical, tendremos en cuenta que la magnitud de la altura del tetraedro está en función de la magnitud de sus aristas. Ésta es el cateto mayor de un triángulo rectángulo, siendo el cateto menor la proyección horizontal de una de las aristas (v-b) y la hipotenusa, la verdadera magnitud de dicha arista.

Octaedro apoyado por un vértice en el plano horizontal

EL OCTAEDRO

El octaedro es un poliedro regular con caras triangulares equiláteras y donde todos los vértices reciben cuatro aristas.

Es el antiprisma regular más simple al ser triangular. 

También es una bipirámide  al poderse obtener uniendo dos pirámides regulares de base cuadrada por sus bases.

OCTAEDRO APOYADO POR UN VÉRTICE EN EL PLANO HORIZONTAL

Cuando un octaedro se representa apoyado por un vértice y con una de sus diagonales perpendicular al plano horizontal de proyección, el contorno aparente de la proyección horizontal es un cuadrado de lado igual a la arista en verdadera magnitud.

 Los lados de este cuadrado son cuatro aristas horizontales que se proyectan en verdadera magnitud sobre el plano horizontal. Las ocho aristas restantes son oblicuas y se proyectan sobre las diagonales del cuadrado.

Las cotas de los vértices, extremos de la diagonal vertical, son cero y la magnitud de la diagonal respectivamente, y los cuatro vértices restantes se encuentran en el plano medio de octaedro, que es horizontal, a una distancia igual a d/2

El Hexaedro

El hexaedro es un poliedro regular formado por seis caras cuadradas, ocho vértices y doce aristas.

Para hacer un hexaedro apoyado por una arista en el plano horizontal hay que seguir los siguientes pasos:

1. Se construye la proyección horizontal del poliedro, que es un rectángulo.

2. Se determina la altura del poliedro.

3. Se dibuja la proyección vertical.

Hexaedro apoyado por una arista en el plano horizonta

Rectas notables del plano

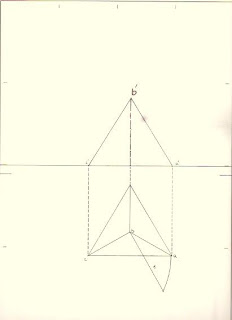
Estas son unos tipos de recta que están contenidas en los planos. Para que una recta esté contenida en un plano, sus trazas tienen que estar en las trazas homónimas del plano.

Hay 4 tipos de rectas notables en un plano:

 

a) Recta Horizontal del Plano: Como su propio nombre indica, cumple una doble condición, es una recta horizontal y está contenida en el plano.

- Por la primera condición, su proyección vertical deber ser paralela a la línea de tierra y tener solamente una traza vertical.

- Por la segunda condición, su traza vertical debe estar contenida en la traza vertical del plano. Además su proyección horizontal debe ser paralela a la traza horizontal del plano en el que está contenida.

También, la distancia entre dos puntos de la recta horizontal se encuentra en verdadera magnitud en su proyección horizontal.

 

 

 

 

 

 

 

 

b) Recta Frontal del plano: Son rectas paralelas al plano vertical de proyección y pertenecientes al plano.

- Solo tiene una traza horizontal, que es paralela a la línea de tierra.

- Su traza horizontal está contenida en la traza horizontal del plano proyección. Además su proyección vertical es paralela a la traza vertical del plano en el que está contenida

También, la distancia entre dos puntos de la recta frontal se encuentra en verdadera magnitud en su proyección vertical.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

c) Recta De Máxima Pendiente: Es un tipo de recta contenida en el plano (sus trazas están contenidas en las trazas del plano) con las siguientes características que la particularizan:

- Su proyección horizontal es perpendicular a la traza horizontal del plano en el que está contenida.

- Es la recta contenida en el plano que forma el mayor ángulo posible con el plano horizontal de proyección

 

 

 

 

 

 

 

 

 

d) Recta De Máxima Inclinación: Es un tipo de recta contenida en el plano (sus trazas están contenidas en las trazas del plano) con las siguientes características que la particularizan:

- Su proyección vertical forma 90º (es perpendicular a) con la traza vertical del plano en el que está contenida.

PLANOS EN DIÉDRICO

INTRODUCCIÓN

Un plano es objeto ideal que solo posee dos dimensiones, y contiene infinitos puntos y rectas; son conceptos fundamentales de la geometría junto con el punto y la recta.

Un plano está definido mediante sus dos trazas: la vertical y la horizontal. Las trazas de un plano son las rectas de intersección con los planos principales (PV y PH).

Una recta pertenece a un plano, si la traza vertical de la recta es un punto de la traza vertical del plano y, además, la traza horizontal de la recta es un punto de la traza horizontal del plano.

Abatimientos

Para obtener, en verdadera magnitud, la representación de una figura contenida en un plano cualquiera, se abate dicho plano sobre uno de los principales.

FORMAS DE DEFINIR UN PLANO

Cuando se habla de un plano, se está hablando del objeto geométrico que no posee volumen, es decir bidimensional, y que posee un número infinito de rectas y puntos. Sin embargo, cuando el término se utiliza en plural, se está hablando de aquel material que es elaborado como una representación gráfica de superficies en diferentes posiciones. Los planos son especialmente utilizados en ingeniería, arquitectura y diseño ya que sirven para diagramar en una superficie plana otras superficies que son regularmente tridimensionales.

Un plano queda definido por los siguientes elementos geométricos:

• Tres puntos no alineados.
• Una recta y un punto exterior a ella.
• Dos rectas paralelas.
• Dos rectas que se cortan.

Los planos suelen nombrarse con una letra del alfabeto griego.

Suele representarse gráficamente, para su mejor visualización, como una figura delimitada por bordes irregulares (para indicar que el dibujo es una parte de una superficie infinita).

PROPIEDADES DEL PLANO

Podemos distinguir seis propiedades:

• Dos planos o son paralelos o se intersecan en una línea.
• Una línea es paralela a un plano o interseca al mismo en un punto o es contenida por el plano mismo.
• Dos líneas perpendiculares a un mismo plano son necesariamente paralelas entre sí.
• Dos planos perpendiculares a una misma línea son necesariamente paralelos entre sí.
• Entre un plano Π cualquiera y una línea no perpendicular al mismo existe solo un plano tal que contiene a la línea y es perpendicular al plano Π.
• Entre un plano Π cualquiera y una línea perpendicular al mismo existe un número infinito de planos tal que contienen a la línea y son perpendiculares al plano Π.

EL PLANO Y SUS DIFERENTES POSICIONES:

Recta horizontal del plano:

-Su traza vertical es paralela a LT

-Todos los puntos de la recta horizontal tienen la misma cota

-Su traza horizontal es paralela a la traza horizontal del plano
-La distancia entre dos puntos de la recta horizontalse encuentra en verdadera magnitud en su proyección horizontal.

Recta oblicua

Es cuando se cruzan en forma inclinada entre ellas, y por lo tanto dividen el plano en cuatro sectores de los cuales dos son iguales, pero distintos de los otros dos que a su vez son iguales entre sí. Es decir que forma con otra línea un ángulo que no es recto.

                                     -Recta horizontal del plano

                                                       Recta oblicua

• Recta de máxima pendiente: Es la recta que perteneciendo al plano forma mayor ángulo con el plano horizontal                 
  Recta frontal: Es una recta paralela al plano frontal de proyección y por lo tanto se proyectará en verdadera magnitud sobre el plano frontal. La verdadera magnitud de esta recta es paralela a la línea de tierra.                                 

                       

                                                  Recta de maxima pendiente 

                     

   Recta frontal del plano

Recta de máxima inclinación: Es la recta del plano que forma mayor ángulo con el plano vertical 

Recta de máxima inclinación

                                                           

RELACIONES DE PERTENENCIA

Relaciones de pertenencia

Punto a recta

Un punto pertenece a una recta cuando las proyecciones homónimas del punto se sitúan en las de la recta. La proyección horizontal (vertical) del punto pertenece a la proyección horizontal (vertical) de la recta.

Recta a plano
Una recta pertenece a un plano cuando las trazas de la recta se sitúan en las trazas del mismo nombre del plano.

Punto a plano
Un punto pertenece a un plano cuando se puede situar en una recta de dicho plano.